다익스트라 알고리즘
다익스트라 알고리즘은 그래프에서 최단거리를 구하는 알고리즘으로, 가중치 그래프에서 한 정점에서 다른 정점과의 최단거리를 구하는 알고리즘 입니다.
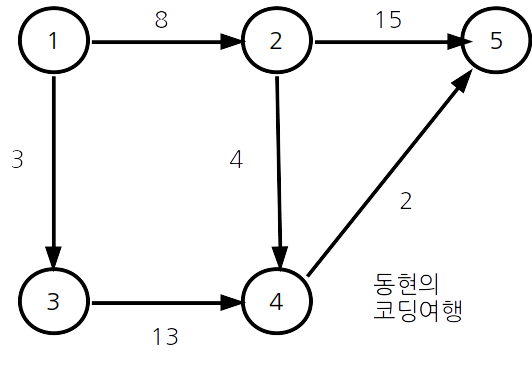
다음과 같이 주어진 그래프를 인접리스트로 구현합니다. 한 노드에 대해 인접한 정점을 (노드번호, 거리) 튜플로 저장합니다.
1 -> (2,8) (3,3)
2 -> (4,4) (5,15)
3 -> (4,13)
4 -> (5,2)
5
위와 같이 인접리스트를 만든후, 최단 거리리스트를 초기화하고 탐색을 시작합니다.
정점 1부터 출발한다고 가정하겠습니다. (INF는 무한대 입니다.)
| 1 | 2 | 3 | 4 | 5 |
| 0 | INF | INF | INF | INF |
그 중 거리가 가장 짧은 1을 채택해서 탐색합니다.
| 1 | 2 | 3 | 4 | 5 |
| 0 | 8 | 3 | INF | INF |
1은 이제 탐색했으므로 방문여부 체크하고 다시 탐색하지 않습니다. 1을 제외한 노드들 중 거리가 짧은 3을 우선적으로 탐색합니다.
| 1 | 2 | 3 | 4 | 5 |
| 0 | 8 | 3 | 3+13 | INF |
3을 거쳐서 4를 가는 것이므로 13을 더해줍니다.
남아 있는 노드들 중 2가 거리가 작으므로 2를 탐색합니다.
| 1 | 2 | 3 | 4 | 5 |
| 0 | 8 | 3 | 16 / 8+4 = 12 | 23 |
2를 탐색했을때 (4,4)이므로 1->2->4 를 거치게 되면 8+4= 12가 됩니다.
그러나 기존에 16이란 값이 있는데, 더 작은 값을 채택해서 12로 결정합니다.
방문하지 않은 노드들 중에서 거리가 12가 가장 낮으므로 4를 탐색합니다.
| 1 | 2 | 3 | 4 | 5 |
| 0 | 8 | 3 | 12 | 23 / 12 + 5 |
(5,5) 이므로 12 + 5 해서 17이 되므로 더 작은 17이 체택됩니다.
이런식으로 5까지 탐색해서 모든 노드의 방문을 마치면 최단거리 탐색이 끝납니다.
최소비용 구하기
문제
N개의 도시가 있다. 그리고 한 도시에서 출발하여 다른 도시에 도착하는 M개의 버스가 있다. 우리는 A번째 도시에서 B번째 도시까지 가는데 드는 버스 비용을 최소화 시키려고 한다. A번째 도시에서 B번째 도시까지 가는데 드는 최소비용을 출력하여라. 도시의 번호는 1부터 N까지이다.
입력
첫째 줄에 도시의 개수 N(1 ≤ N ≤ 1,000)이 주어지고 둘째 줄에는 버스의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 M+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가 주어진다. 그리고 그 다음에는 도착지의 도시 번호가 주어지고 또 그 버스 비용이 주어진다. 버스 비용은 0보다 크거나 같고, 100,000보다 작은 정수이다.
그리고 M+3째 줄에는 우리가 구하고자 하는 구간 출발점의 도시번호와 도착점의 도시번호가 주어진다. 출발점에서 도착점을 갈 수 있는 경우만 입력으로 주어진다.
출력
첫째 줄에 출발 도시에서 도착 도시까지 가는데 드는 최소 비용을 출력한다.
예제 입력 1
5
8
1 2 2
1 3 3
1 4 1
1 5 10
2 4 2
3 4 1
3 5 1
4 5 3
1 5
예제 출력 1
4파이썬 코드
adjacent는 인접리스트를 의미합니다.
다익스트라는 최단거리 알고리즘인데, 거리 = 비용과 치환해서 생각하면 쉽게 풀릴수 있습니다.
거리가 가장 작은 노드를 골라서 탐색해야되는데, 거리가 작은 노드를 고르는게 시간 복잡도가 큽니다.
그러므로 우선순위 큐를 사용합니다.
(거리, 노드번호) 이렇게 튜플로 넣으면 첫째항인 거리를 우선순위로 내림차순으로 정렬합니다.
#dijkstra
import sys
from queue import PriorityQueue
input = sys.stdin.readline
n = int(input())
m = int(input())
infinity = 1
adjacent = [[]for _ in range(n+1)]
visited = [False] * (n+1)
for i in range(m):
n1,n2,w = map(int, input().split())
adjacent[n1].append((n2,w))
infinity+=w
start , end = map(int,input().split())
dist = [infinity] * (n+1)
visited = [False]*(n+1)
queue = PriorityQueue()
queue.put((0,start))
dist[start] = 0
#다익스트라 시작
while not queue.empty():
node = queue.get()[1]
if visited[node]:
continue
visited[node] = True
for i in adjacent[node]:
distance = dist[node] + i[1]
if dist[i[0]] > distance:
dist[i[0]] = distance
queue.put((distance , i[0]))
print(dist[end])'알고리즘 PS (백준) > 🐍 Python (파이썬)' 카테고리의 다른 글
| [백준 1504] 다익스트라(Dijkstra) - 파이썬 (Python) (1) | 2022.10.14 |
|---|---|
| [백준 1238] 다익스트라(Dijkstra) - 파이썬 (Python) (3) | 2022.10.14 |
| 파이썬(Python) 다익스트라 개념과 예제-백준 1753번 (1) | 2022.10.14 |
| [백준 1016] 파이썬(Python) 제곱ㄴㄴ수 - 에라토스테네스의 체 (0) | 2022.10.10 |
| [파이썬 Python] 에라토스테네스의 체(소수 구하기) 개념과 예제 - (백준 1747) (0) | 2022.10.10 |




댓글