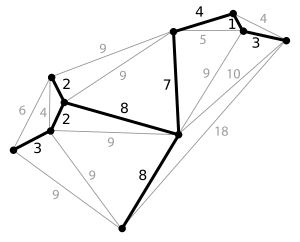
최소 신장 트리 : 최소 신장 트리는 모든 노드가 연결되도록 간선을 그은 트리의 가중치의 합이 가장 작은 것을 말합니다. 가중치의 값이 최소가 돼야되기 때문에 사이클은 없어야 합니다.
크루스칼 알고리즘
크루스칼 알고리즘은 최소 신장 부분 트리를 찾는 알고리즘으로 가중치가 가장 낮은 엣지를 순서대로 고르지만, 사이클이 안생기도록 고르는 알고리즘입니다.
변의 개수를 E, 꼭짓점의 개수 V라고 하면 이 알고리즘은O(E\log V)의 시간복잡도를 가집니다.
1. 엣지리스트 초기화 하기
엣지들을 가중치가 낮은것 순서대로 뽑을 것이므로 리스트에다가 넣고, 나중에 정렬해줍니다.
2. 유니온 파인드 알고리즘 적용시키기
유니온 파인드는 쉽게 말해서 집합을 구현하는 알고리즘입니다. 아래 코드를 보시면 겉핥기로 이해되실 것입니다 (크루스칼 포스트이므로 상세하게 설명은 안하겠습니다.)
n, m = map(int, sys.stdin.readline().rstrip().split())
parent = [i for i in range(n+1)]
def get_parent(x):
if parent[x] == x:
return x
parent[x] = get_parent(parent[x]) # get_parent 거슬러 올라가면서 parent[x] 값도 갱신
return parent[x]
def union_parent(a, b):
a = get_parent(a)
b = get_parent(b)
if a < b: # 작은 쪽이 부모가 된다. (한 집합 관계라서 부모가 따로 있는 건 아님)
parent[b] = a
else:
parent[a] = b
def same_parent(a, b):
return get_parent(a) == get_parent(b)이 알고리즘 형식을 더 간단하게 해서 구현할 것 입니다.
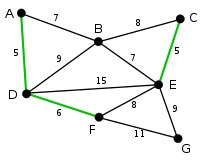
엣지들이 있을때 가중치가 가장 낮은 엣지를 우선적으로 선택해서 차례대로 연결합니다.
만약에 연결하면 사이클이 생기면, 건너뛰고 다음 엣지부터 검토합니다.
사이클이 생기는 지 여부는 유니온 파인드 알고리즘을 통해 판별할 수 있습니다.
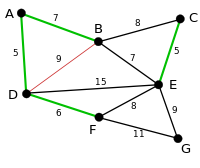
예를 들면 가중치가 9인 빨간색 엣지의 양끝 노드를 보면 B,D인데 둘다 같은 유니온(집합)에 속해있기 때문에 사이클이 생기므로 건너뛰고 다음 엣지를 살펴봅니다.

N이 노드의 갯수라고 할때, 탐색을 전부완료하면 N-1개의 엣지가 있어야되고, 모든 노드들이 한 유니온으로 연결되어있어야합니다.
엣지리스트를 내림차순으로 정렬하고 하나씩 뽑아서 유니온이 아닌 노드를 연결하는 엣지마다 적용 시켜주면 됩니다.
edges.sort(key = lambda x : x[2])
i = 0
while cnt<n-1:
w,a,b = edges[i][0] , edges[i][1], edges[i][2]
if find(a) != find((b)):
cnt += 1
weight += w
union(a, b)
i+=1
print(weight)최소 스패닝 트리
문제
그래프가 주어졌을 때, 그 그래프의 최소 스패닝 트리를 구하는 프로그램을 작성하시오.
최소 스패닝 트리는, 주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 말한다.
입력
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이 가중치 C인 간선으로 연결되어 있다는 의미이다. C는 음수일 수도 있으며, 절댓값이 1,000,000을 넘지 않는다.
그래프의 정점은 1번부터 V번까지 번호가 매겨져 있고, 임의의 두 정점 사이에 경로가 있다. 최소 스패닝 트리의 가중치가 -2,147,483,648보다 크거나 같고, 2,147,483,647보다 작거나 같은 데이터만 입력으로 주어진다.
출력
첫째 줄에 최소 스패닝 트리의 가중치를 출력한다.
예제 입력 1
3 3
1 2 1
2 3 2
1 3 3
예제 출력 1
3파이썬 코드
앞에서 설명한 방법 그대로 코드로 옮기면 됩니다.
heap리스트에서 정렬할때, (s,e,가중치) 튜플이 들어가있으므로 가중치를 기준으로 정렬할때, 저 람다식으로 정렬할 수 있습니다.
3번째이므로 2번 인덱스입니다.
# 최소 신장 트리
# 크루스칼
heap = []
n, m = map(int, input().split())
for _ in range(m):
heap.append(list(map(int, input().split())))
cnt = 0
weight = 0
nodes = [0] * (n+1)
for i in range(1,n+1):
nodes[i] = i
def find(a):
if nodes[a] ==a:
return a
else:
nodes[a] = find(nodes[a])
return nodes[a]
def union(a,b):
a = find(a)
b = find(b)
if a!=b:
if a<b:
nodes[b] = a
else:
nodes[a] = b
heap.sort(key = lambda x : x[2])
i = 0
while cnt<n-1:
w,a,b = heap[i][0] , heap[i][1], heap[i][2]
if find(a) != find((b)):
cnt += 1
weight += w
union(a, b)
i+=1
print(weight)'알고리즘 PS (백준) > 🐍 Python (파이썬)' 카테고리의 다른 글
| [백준 11437] 최소 공통 조상(LCA) 알고리즘(기본) - 파이썬(Python) (0) | 2023.01.04 |
|---|---|
| [백준 1414] 크루스칼 알고리즘(Kruskal , 최소신장트리) - 파이썬(Python) (0) | 2023.01.04 |
| [백준 11780] 플로이드-워셜 알고리즘 - 파이썬(Python) (0) | 2022.12.31 |
| 파이썬(Python) 플로이드-워셜(Floyd-Warshall) 개념과 예제 (백준 11404) (0) | 2022.12.31 |
| [백준 1219] 벨만-포드 알고리즘 - 파이썬 Python (0) | 2022.12.31 |




댓글