분할정복 알고리즘이란?
분할정복은 여러 알고리즘 한번에 해결할 수 없는 문제를 잘게 쪼개서 해결할 만한 부분문제들로 만든다음에,
그 문제들을 해결하면서 정복해가며 문제를 해결하는 방법으로 보통 재귀함수로 구현합니다.
문제를 잘게 쪼개서 해결한다고 하니까 동적 계획법(DP, 다이나믹 프로그래밍)이랑 똑같은것이 아닌가? 라고 생각이 들것입니다.
확실히 DP의 하향식 접근법이랑 유사한 부분이 많지만 부분문제가 중복되지 않는 부분에서 차이가 있습니다.
DP문제, 예를 들어 피보나치 수열 구하기 등은 부분문제가 중복돼서 다른 상위 문제를 푸는데 해결되기 때문에 메모리제이션 기법을 사용합니다. (예를 들어 a10을 구하기 위해서 부분문제를 a9 a8로 나눴을때, a8의 부분문제 a7은 a9를 해결하는데도 쓰이므로 중복됩니다. 그래서 결과를 저장하는 메모리제이션 기법을 사용하는 것입니다)
그러나 분할정복은 부분문제가 중복되지 않으므로 결과를 기억할 필요도 없고 메모리제이션도 이용하지 않습니다.
분할정복을 기반으로 하는 알고리즘엔 퀵소트나 병합정렬등 많은 알고리즘이 있는데,
이번엔 분할정복을 이용한 거듭제곱을 이용하겠습니다.
분할정복을 이용한 거듭제곱
C^n연산은 C를 n번 곱하므로 O(N)이지만, 분할정복을 사용하면 O(logN)에 거듭제곱 값을 구할 수 있습니다.
아래 점화식을 이용해서 적용합니다.
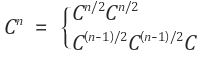
파이썬 코드로 적용시키면 아래와 같습니다. (a**n)하면 a^n이 됩니다.
def dac(t):
if t==1:
return n
if t%2==0:
return dac(t//2)**2
else:
return (dac(t//2)**2)*n예제 - 백준 1629
자연수 A를 B번 곱한 수를 알고 싶다. 단 구하려는 수가 매우 커질 수 있으므로 이를 C로 나눈 나머지를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 A, B, C가 빈 칸을 사이에 두고 순서대로 주어진다. A, B, C는 모두 2,147,483,647 이하의 자연수이다.
출력
첫째 줄에 A를 B번 곱한 수를 C로 나눈 나머지를 출력한다.
예제 입력
10 11 12
예제 출력
41629 파이썬 코드
위에서 보여준 점화식 그대로 재귀함수에 적용해서 해결할 수 있습니다.
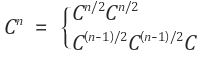
(a*b)%c는 ((a%c)*(b%c))%c 같다는 나머지 정리가 있으므로, 거듭제곱하려는 수를 미리 c로 나눈 나머지로해서 거듭제곱을해서 수의 크기를 미리 줄여서 연산합니다.
a,b,c = map(int, input().split())
# 나머지 정리
# (a*b)%c는 ((a%c)*(b%c))%c 같다
n=a%c
def dac(t):
if t==1:
return n
if t%2==0:
return (dac(t//2)**2)%c
else:
return ((dac(t//2)**2)*n)%c
print(dac(b))'알고리즘 PS (백준) > 🐍 Python (파이썬)' 카테고리의 다른 글
| [백준 16236] 아기 상어 - 파이썬(Python) BFS풀이 (0) | 2023.09.24 |
|---|---|
| [백준 10830] 분할정복을 이용한 행렬 제곱 - 파이썬(Python) (0) | 2023.09.24 |
| [백준 17144] 미세먼지 안녕! - 파이썬(Python) (0) | 2023.09.23 |
| [백준 14502] 연구소 - 파이썬(Python) BFS 풀이 (0) | 2023.09.23 |
| [백준 11437] 최소 공통 조상(LCA) 알고리즘(기본) - 파이썬(Python) (0) | 2023.01.04 |




댓글