행렬 제곱
문제
크기가 N*N인 행렬 A가 주어진다. 이때, A의 B제곱을 구하는 프로그램을 작성하시오. 수가 매우 커질 수 있으니, A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다.
입력
첫째 줄에 행렬의 크기 N과 B가 주어진다. (2 ≤ N ≤ 5, 1 ≤ B ≤ 100,000,000,000)
둘째 줄부터 N개의 줄에 행렬의 각 원소가 주어진다. 행렬의 각 원소는 1,000보다 작거나 같은 자연수 또는 0이다.
출력
첫째 줄부터 N개의 줄에 걸쳐 행렬 A를 B제곱한 결과를 출력한다.
예제 입력
2 5
1 2
3 4
예제 출력
69 558
337 406행렬의 거듭제곱
행렬의 제곱은 아래와 같이 똑같은 정사각행렬을 내적시키는 것을 행렬의 제곱이라고 합니다.
그럴려면 벡터/행렬의 내적을 알아야되는데요, 선형대수학 내용이지만 문제 풀 수 있을정도로 간략하게 설명해드리겠습니다.
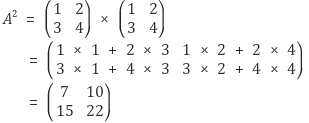
벡터의 내적
벡터 v1, v2가 있다고 할때, v1 = [x1, y1], v2= [x2, y2] 이 두 벡터를 내적하면 x1*x2 + y1*y2라는 상수 값이 나옵니다.
이것을 벡터의 내적이라고 하는데, 행렬은 이 벡터들이 행을 이루면서 겹겹이 붙여져있는것을 말합니다.
행렬의 내적
행렬의 내적이란 아래 그림과 같이 A행렬의 행과 B행렬의 열에 해당하는 각 벡터들을 모든 조합으로 내적시키는 것인데요, A의 행에 해당하는 행과 B에 열에 해당하는 위치로 그 벡터의 내적의 값을 위치시키는 것입니다.
아래 그림처럼 색칠된 두 벡터가 내적한다고 하면, 3번째 행의 벡터와 3번째 열의 벡터가 내적을 했으므로 그 계산값은 결과행렬의(3,3) 위치에 위치하게 됩니다.

그래서 결과행렬의 (i,j)위치에 있는 원소는 ai1*b1j + ai2*b2j + ai3*b3j + ai4*b4j ..... 연산으로 구할 수 있고, 11,22값들을 k로 치환해서 시그마로 묶으면 일반항이 나옵니다.
그 일반항을 핵심으로 내적하는 파이썬 코드를 작성하면 아래와 같습니다.
행렬내적 파이썬 코드
각 벡터를 내적하고 나온값을 add에 저장하고 행렬에 넣습니다.
# 행렬 내적
def innerMat(m1, m2):
result = [[0]*n for _ in range(n)]
for i in range(n):
for j in range(n):
add = 0
for k in range(n):
add += (m1[i][k]*m2[k][j])
result[i][j] = add
return result분할정복 알고리즘이란?
분할정복은 여러 알고리즘 한번에 해결할 수 없는 문제를 잘게 쪼개서 해결할 만한 부분문제들로 만든다음에,
그 문제들을 해결하면서 정복해가며 문제를 해결하는 방법으로 보통 재귀함수로 구현합니다.
문제를 잘게 쪼개서 해결한다고 하니까 동적 계획법(DP, 다이나믹 프로그래밍)이랑 똑같은것이 아닌가? 라고 생각이 들것입니다.
확실히 DP의 하향식 접근법이랑 유사한 부분이 많지만 부분문제가 중복되지 않는 부분에서 차이가 있습니다.
DP문제, 예를 들어 피보나치 수열 구하기 등은 부분문제가 중복돼서 다른 상위 문제를 푸는데 해결되기 때문에 메모리제이션 기법을 사용합니다. (예를 들어 a10을 구하기 위해서 부분문제를 a9 a8로 나눴을때, a8의 부분문제 a7은 a9를 해결하는데도 쓰이므로 중복됩니다. 그래서 결과를 저장하는 메모리제이션 기법을 사용하는 것입니다)
그러나 분할정복은 부분문제가 중복되지 않으므로 결과를 기억할 필요도 없고 메모리제이션도 이용하지 않습니다.
분할정복을 기반으로 하는 알고리즘엔 퀵소트나 병합정렬등 많은 알고리즘이 있는데,
이번엔 분할정복을 이용한 거듭제곱을 이용하겠습니다.
분할정복을 이용한 거듭제곱
C^n연산은 C를 n번 곱하므로 O(N)이지만, 분할 정복을 사용하면 O(logN)에 거듭제곱 값을 구할 수 있습니다.
아래 점화식을 이용해서 적용합니다.
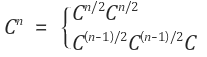
예를 들어 C^8승을 구할때 C를 8번 곱하는 방법 보다는 C^2을 제곱해서 C^4를 구하고, 또 이것을 제곱해서 C^8을 구하면 훨씬 적은 연산으로 구할 수 있습니다.
파이썬 코드로 적용시키면 아래와 같습니다.
def dac(t):
if t==1:
return n
if t%2==0:
return dac(t//2)**2
else:
return (dac(t//2)**2)*n
행렬의 제곱도 일일히 행렬들을 내적하면, 내적하는 데 시간이 오래 걸리므로 분할정복 거듭제곱 알고리즘을 이용해 더 적은 내적횟수로 제곱을 구할 수 있습니다.
파이썬(Python) 코드
행렬의 제곱이 간단하지 않으므로 점화식에서 n이 홀수에 해당하는 내용을 아래와 같이 바꿨습니다. (기존 점화식대로면 내적을 세번해야됩니다..)
C^n = C(n-1) * C (n이 홀수)
짝수일 경우에는 바로 내적하는 코드(innerMat 함수 내용 그대로)를 작성했습니다.
import sys
input = sys.stdin.readline
n, b = map(int, input().split())
mat = [list(map(lambda x: int(x) % 1000, input().split())) for _ in range(n)]
# 행렬 내적
def innerMat(m1, m2):
result = [[0]*n for _ in range(n)]
for i in range(n):
for j in range(n):
add = 0
for k in range(n):
add += (m1[i][k]*m2[k][j]) % 1000
result[i][j] = add % 1000
return result
def squareMat(mat, b):
if b == 1:
return mat
if b % 2 == 0:
mat = squareMat(mat, b//2)
result = [[0]*n for _ in range(n)]
for i in range(n):
for j in range(n):
add = 0
for k in range(n):
add += (mat[i][k]*mat[k][j]) % 1000
result[i][j] = add % 1000
return result
else:
return innerMat(squareMat(mat, b-1), mat)
ans = squareMat(mat, b)
for i in range(n):
print(*ans[i])'알고리즘 PS (백준) > 🐍 Python (파이썬)' 카테고리의 다른 글
| [백준 2448] 별 찍기 - 11 (파이썬 Python) (0) | 2023.09.25 |
|---|---|
| [백준 16236] 아기 상어 - 파이썬(Python) BFS풀이 (0) | 2023.09.24 |
| 파이썬(Python) 분할정복 개념과 예제 - 백준 1629 (1) | 2023.09.24 |
| [백준 17144] 미세먼지 안녕! - 파이썬(Python) (0) | 2023.09.23 |
| [백준 14502] 연구소 - 파이썬(Python) BFS 풀이 (0) | 2023.09.23 |




댓글