정규화(Normalization)란?
정규화는 데이터베이스 설계 시 데이터의 중복을 최소화하고, 데이터의 무결성을 유지하기 위해 테이블을 구조적으로 분해하는 과정이다. 정규화를 통해 데이터 저장 공간의 낭비를 줄이고, 삽입/삭제/갱신 이상(Anomaly)을 방지할 수 있다.
정규화의 목적
- 중복 데이터 제거
- 데이터 무결성 유지
- 삽입/삭제/갱신 이상(Anomalies) 방지
- 테이블 간의 명확한 관계 설정
정규화 과정 (Normal Forms)
정규화는 여러 단계로 구성되며, 각 단계는 이전 단계보다 더 높은 수준의 정규성을 보장한다:
- 제1정규형(1NF): 모든 속성 값이 원자값(Atomic Value)으로 되어 있어야 함
- 제2정규형(2NF): 1NF를 만족하고, 부분 함수 종속 제거
- 제3정규형(3NF): 2NF를 만족하고, 이행적 함수 종속 제거
- BCNF(Boyce-Codd 정규형): 모든 결정자가 후보키인 상태
- 제4정규형(4NF): 다치 종속 제거
- 제5정규형(5NF): 조인 종속 제거
스키마 Composition 시 중복 발생 가능성

- instructor와 department를 inst_dept라는 하나의 릴레이션으로 병합한다고 가정할 때,
- 특정 학과에 여러 교수가 소속되어 있으면 building, budget 등의 정보가 반복됨
- → 정보의 중복이 발생하게 됨
중복 없는 스키마 병합의 예
- sec_class(sec_id, building, room_number) 와section(course_id, sec_id, semester, year)를 natural join(병합)하여section(course_id, sec_id, semester, year, building, room_number)로 구성
- 이 경우 sec_id가 기본 키로 중복을 제거해주기 때문에 정보의 반복이 없음
작은 스키마로의 분해
테이블을 쪼갤때는 중복이 있으니까 쪼갰지만 속성에 관한 함수 종속성 고려 후보키는 중복이 없고, 다른 속성을 결졍할수 있으니까 함수 종속성이 성립한다.
같은 후보키라면 -> 다른 속성도 같다!
처음부터 병합된 스키마로 시작한 경우
- inst_dept 테이블에서 설계를 시작했다고 가정
- 이 스키마를 instructor와 department로 분해해야 할지 판단하려면 함수 종속성(functional dependency) 분석 필요
functional dependency : 하나의 속성이 다른 속성을 결정하면 성립한다
예시 함수 종속성:
- dept_name → building, budget
- 그러나 dept_name은 inst_dept의 후보 키(candidate key) 가 아니며, 하나의 학과에 여러 명의 교수가 있을 수 있기 때문에building과 budget 정보가 반복됨 → 분해 필요성을 시사함
손실 분해(A Lossy Decomposition)의 예
분해가 항상 바람직하지는 않는다.
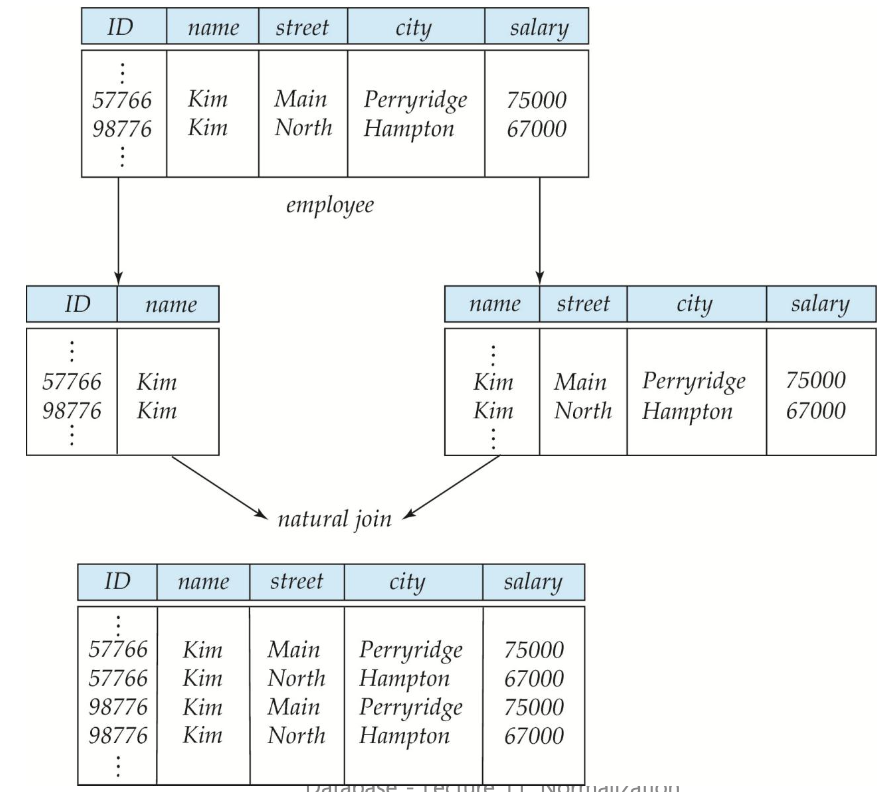
name 속성으로 분해한다면, name은 후보키도 아니고 함수 종속성이 없으므로 Lossy decomposition이 된다. (다시 복원을 할 수 없다)
예시:
- employee(ID, name, street, city, salary)를 employee1(ID, name)과 employee2(name, street, city, salary)로 분해한 경우
- 원래 테이블을 복원할 수 없게 됨 → 이는 정보 손실 분해(lossy decomposition)
무손실 분해(Lossless-Join Decomposition)의 예

테이블을 분해 후 naural join을 해서 원본 테이블 복원할 수 있을때. -> 우리의 목표!
- 테이블 R(A, B, C)를 R1(A, B), R2(B, C)로 분해하는 경우 → 이는 무손실 분해가 될 수 있음
제1 정규형 (First Normal Form, 1NF)
- 속성의 도메인이 원자적(atomic) 이어야 함 : 속성값을 쪼갤 수 없다.
- 원자적이지 않은 도메인 예시: 이름의 집합, 복합 속성 등
- 모든 속성의 도메인이 원자적인 경우, 해당 릴레이션은 제1 정규형에 속함
- 비원자적 값은 중복 데이터를 유발하므로 일반적으로 피해야 하며, 모든 릴레이션은 1NF에 있다고 가정함
정규형 판단의 목표
- 릴레이션 R이 좋은 형태(good form) 인지 판단
- 좋지 않다면 {R1, R2, ..., Rn}으로 분해
- 각 릴레이션은 좋은 형태여야 함
- 전체는 무손실 분해가 되어야 함
이론의 기반:
- 함수 종속성 (Functional Dependencies)
- 다중값 종속성 (Multivalued Dependencies)
함수 종속성 (Functional Dependencies)
- 릴레이션 스키마 R에서, α ⊆ R, β ⊆ R일 때
- 임의의 합법적 릴레이션 r(R)에 대해두 튜플 t1, t2가 α에 대해 같은 값을 가진다면,
- β에 대해서도 같은 값을 가져야 함
t1[α] = t2[α] → t1[β] = t2[β]
- 즉,
- 두 튜플 t1, t2가 α에 대해 같은 값을 가진다면,
- α → β는 다음 조건을 만족해야 함:
예시 1

- 테이블 r(A, B)에서 A → B는 성립하지 않지만, B → A는 성립할 수 있음
예시 2
| 주민등록번호 (A) | 이름 (B) |
| 123456-7890123 | 김철수 |
| 123456-7890123 | 김철수 |
| 123456-7890100 | 김철수 |
- 여기서 주민등록번호 → 이름, 즉 A → B는 항상 성립
- 주민등록번호가 같으면 반드시 이름도 같다
- 반대로 B → A는 성립하지 않음
- 이름이 같다고해서, 주민등록번호가 같다는 보장이 없다.
함수 종속성과 키의 관계
- 함수 종속성은 키 개념의 일반화
- K가 슈퍼 키이면: K → R (relation의 모든 attribute)
- K가 후보 키이면:
- K → R을 만족하고
- K의 어떤 부분집합 α에 대해서도 (K - α ) → R이 성립하지 않음
- 최소한의 속성으로 구성한게 후보키이므로 두 조건을 만족해야된다.
예시:
- 스키마 inst_dept(ID, name, salary, dept_name, building, budget)
- 기대되는 함수 종속성:dept_name → building, ID → building
- 기대되지 않는 함수 종속성:dept_name → salary
자명한 함수 종속성 (Trivial Functional Dependency)
- 모든 릴레이션 인스턴스에서 항상 만족되는 함수 종속성
- 예시: α → β
- ID, name → ID
- name → name
- 일반적으로 β ⊆ α인 경우(β가 α의 부분집합), α → β는 자명한 종속성
함수 종속성의 폐쇄(Closure ⁺)
a가 b를 결정하고 b가 c를 결정할 경우, a->c에 결정 되겠구나 추측이 가능하다. 이미 제공된 종속성을 가지고 새로운 함수 종속성을 만들었을때 closure 종속성이라 한다 F 이용해서 만든 모든 함수 종속성을 F⁺ 라고 한다 ( closure of F )
- 주어진 함수 종속성 집합 F로부터 추론 가능한 모든 함수 종속성의 집합을 F⁺라고 한다
- 예:
- A → B, B → C가 주어졌다면A → C를 유도할 수 있음 → 이 역시 F⁺에 포함 F⁺ 는 F의 superset 이다. (F⁺이 모든 함수 종속성을 포괄하는 집합)
함수 종속성의 성질
- 부분집합 속성 (Subset property / Trivial): Y ⊆ X이면 X → Y
- 증강 법칙 (Augmentation): X → Y이면, XZ → YZ
- 추이성 (Transitivity): X → Y, Y → Z이면 X → Z
- 합집합 (Union): X → Y, X → Z이면 X → YZ
- 분해 (Decomposition): X → YZ이면 X → Y, X → Z
- 의사 추이성 (Pseudo-transitivity): X → Y, WY → Z이면 WX → Z
보이스-코드 정규형 (BCNF, Boyce-Codd Normal Form)
릴레이션 스키마 R이 함수 종속성 집합 F에 대해 BCNF를 만족하려면,
F⁺에 있는 모든 함수 종속성 α → β에 대해 다음 중 하나를 만족해야 한다 (OR):
- α → β는 자명한(Trivial) 종속성이다 (β ⊆ α)
- α는 R의 슈퍼 키이다
BCNF 위반 예시
릴레이션: inst_dept(ID, name, salary, dept_name, building, budget)
- ID -> R : Trivial하지 않지만, 후보키이자 수퍼키 이다. 그러므로 BCNF를 위반하지 않는다
- dept_name → building, budget 이라는 함수 종속성이 성립하지만, Trivial하지도 않고 dept_name은 슈퍼 키가 아니다. -> 두 조건을 둘다 위배하므로 BCNF 위반에 해당함.
BCNF 분해(Decomposing)
어떤 비자명한(non-trivial) 함수 종속성 α → β가 BCNF를 위반할 경우, R을 다음 두 릴레이션으로 분해한다:
- (α ∪ β)
- (R − (β − α)) : 공통 속성을 빼는 것이다.
예시:
α = dept_name, β = {building, budget}
→ 분해 결과: inst_dept는 아래 대체된다.
- (dept_name, building, budget)
- (ID, name, salary, dept_name)
BCNF 분해 예시
릴레이션:
HR(DPT_NO, MGR_NO, EMP_NO, EMP_NAME, PHONE)
함수 종속성 집합 F:
- DPT_NO → MGR_NO
- DPT_NO → PHONE
- EMP_NO → EMP_NAME
BCNF 위반: DPT_NO → MGR_NO
→ 분해:
- HR1(DPT_NO, MGR_NO) : (α ∪ β)
- HR2(DPT_NO, EMP_NO, EMP_NAME, PHONE) : (R − (β − α))
하지만 HR2에도 여전히 BCNF 위반이 존재할 수 있으므로 추가 분해 필요
BCNF의 한계: 과도한 분해

함수 종속성:
- AB → C, C → B
- 예: A = street, B = city, C = zip
- A는 AB의 부분집합이므로 AB -> A, AB는 수퍼키가 된다.
- C → B에서 C는 A를 결정할 수 없다 그러므로 수퍼키가 아니다-> BCNF 분해
- (α ∪ β) : (BC)
- (R − (β − α)) : (AC)
이 경우 BCNF에 따라 분해하면 AC와 BC로 나누게 되며,
원래의 AB → C를 보존할 수 없음 → 종속성 보존 불가!

해결책: 제3정규형 (3NF, Third Normal Form)
BCNF는 항상 종속성 보존을 보장하지 않음
→ 그래서 3NF라는 더 약한 정규형이 사용됨
3NF는 약간의 중복을 허용하지만:
- 종속성 검증이 개별 릴레이션에서 가능
- 항상 무손실 조인과 종속성 보존을 만족하는 분해가 가능
3NF 정의
릴레이션 R이 함수 종속성 집합 F에 대해 3NF를 만족하려면,
F⁺에 있는 모든 α → β에 대해(α → β in F⁺) 다음 중 하나를 만족해야 한다(OR):
- α → β는 자명한 종속성이다 (β ⊆ α)
- α는 R의 슈퍼 키이다
- β − α에 있는 모든 속성은 R의 후보 키에 속한다
→ BCNF를 만족하는 릴레이션은 항상 3NF도 만족함
3NF의 중복 문제
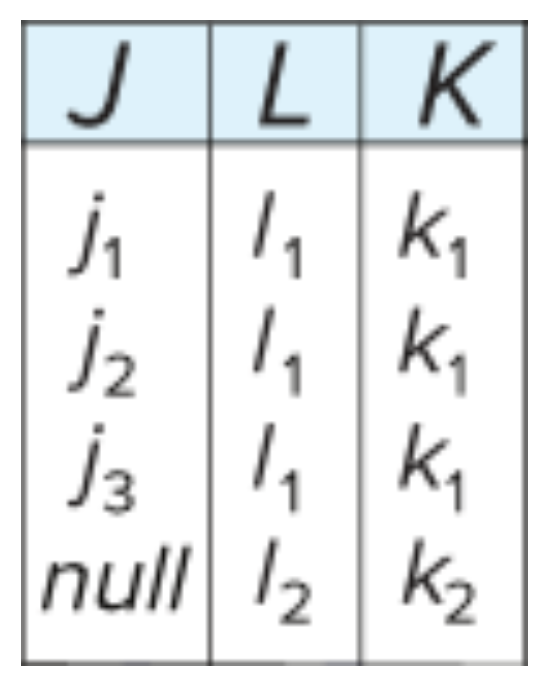
릴레이션: R = (J, K, L) 함수 종속성: F = {JK → L, L → K}
이 릴레이션은 3NF를 만족하지만:
- 정보의 반복이 발생하고
- 일부 관계는 NULL 값으로 표현해야 하는 문제가 있음
BCNF vs 3NF 비교
3NF의 장점
- 항상 무손실 분해 + 종속성 보존 가능
- 함수 종속성 검증이 개별 릴레이션 단위에서 가능
3NF의 단점
- 정보의 반복 발생 가능
- NULL 값 사용 필요할 수 있음
정규화의 목적
- 저장 공간 절약
- 더 빠른 업데이트
- 데이터 불일치(inconsistency) 감소
- 명확한 데이터 관계
- 데이터 추가 용이
- 유연한 구조 제공
관계형 설계의 목표
- BCNF 만족
- 무손실 조인 (테이블을 쪼갰을때 복구가 가능하도록)
- 종속성 보존 이 세 가지를 모두 만족하지 못할 경우:
- 종속성 보존 포기 (BCNF 유지)
- 중복 허용 (3NF 사용)
참고: SQL에서는 슈퍼 키가 아닌 속성을 기준으로 한 함수 종속성을 명시할 수 없으므로,
설계 수준에서의 종속성 검증이 중요하다.
함수 종속성 이론 (Functional-Dependency Theory)
주어진 함수 종속성 집합 F로부터 논리적으로 유도될 수 있는 모든 함수 종속성을 찾아내는 이론이다.
이러한 유도된 전체 함수 종속성의 집합을 폐쇄(closure) 라고 한다.
함수 종속성 집합의 폐쇄 (Closure of a Set of Functional Dependencies)
F⁺는 주어진 함수 종속성 집합 F로부터 Armstrong의 공리(Axioms) 를 반복적으로 적용하여 도출한다.
Armstrong의 공리
- 반사성 (Reflexivity): β ⊆ α 이면, α → β
- 증강 (Augmentation): α → β 이면, γα → γβ
- 추이성 (Transitivity): α → β, β → γ 이면, α → γ
이 규칙들은 다음의 특성을 만족한다:
- Sound: 실제로 성립하는 종속성만 생성
- Complete: 모든 가능한 종속성을 생성 가능
예시
스키마 R = (A, B, C, G, H, I)
F = { A → B, A → C, CG → H, CG → I, B → H }
- A → H
- A → B, B → H를 이용한 추이성으로 유도
- AG → I
- A → C에 G를 증강하면 AG → CG
- CG → I와 연결하여 AG → I
- CG → HI
- CG → I를 증강하여 CG → CGI
- CG → H도 증강하여 CGI → HI
- 두 관계를 이용한 추이성으로 CG → HI 유도
추가 규칙
이 규칙들도 Armstrong 공리에서 유도 가능하다:
- 합집합 (Union): α → β, α → γ 이면 α → βγ
- 분해 (Decomposition): α → βγ 이면 α → β, α → γ
- 의사 추이성 (Pseudotransitivity): α → β, γβ → δ 이면 αγ → δ
종속성 보존 (Dependency Preservation)
분해된 릴레이션 집합 포함된 함수 종속성 집합 Fi을 나열 했을때
분해가 종속성 보존을 만족하려면:
- (F1 ∪ F2 ∪ ... ∪ Fn)+ = F+
종속성 보존이 되지 않으면,
업데이트 시 함수 종속성 위반 여부 확인을 위해 조인 연산이 필요하므로 비용이 크다.
→ 항상 3NF로 무손실 조인 + 종속성 보존 분해가 존재함
전체 데이터베이스 설계 과정
- E-R 다이어그램을 릴레이션 스키마 R로 변환
- 경우에 따라 R이 모든 attribute를 포함하는 하나의 큰 릴레이션일 수 있음
- 정규화(Normalization) 를 통해 R을 더 작고 의미 있는 릴레이션으로 분해
잘 설계된 E-R 다이어그램이라면 추가 정규화가 필요 없을 수 있음
하지만 현실에서는 종종 비키 속성에서 다른 속성으로의 함수 종속성이 존재
예시:
employee(entity) → 속성: department_name, building
→ 함수 종속성: department_name → building
→ 좋은 설계라면 department를 별도 entity로 정의해야 함
성능 향상을 위한 비정규화 (Denormalization for Performance)
정규화를 통해 데이터 일관성을 보장하지만, join을 수행 시 오버헤드가 발생한다. 조회 성능 향상을 위해 비정규화된 스키마 사용을 고려할 수 있음
예시:
- 과목의 course_id, title과 함께 prereq 정보를 보여줘야 하는 경우
- 정규형에서는 course와 prereq를 조인해야 함
대안 1: 비정규화된 릴레이션 사용
- course와 prereq의 모든 속성을 포함하는 단일 릴레이션 구성
- 장점: 빠른 조회
- 단점:
- 더 많은 저장 공간 필요
- 업데이트 시 불필요한 시간 소모
- 프로그래머가 직접 복잡한 코드 관리해야 하며 오류 가능성 존재
대안 2: 물리 뷰(Materialized View) 사용
- course와 prereq를 조인한 결과를 물리 테이블 형태로 저장
- 장점: 프로그래머가 따로 코드를 작성하지 않아도 됨, 오류 방지 가능
- 단점: 공간 소모 및 업데이트 성능 문제는 동일
요약
- 함수 종속성 이론은 데이터 정규화를 위한 이론적 기초 제공
- Armstrong 공리를 활용해 유도된 종속성(F⁺)을 분석
- BCNF는 이상적이나 종속성 보존이 불가능할 수 있음
- 3NF는 항상 무손실 조인과 종속성 보존을 보장
- 성능 최적화를 위해 비정규화 또는 물리 뷰 도입을 고려할 수 있음
'CS 지식 > 데이터베이스' 카테고리의 다른 글
| [데이터베이스] 스토리지 종류와 DB 파일 물리적 저장 방식 (Slotted Page 구조) (1) | 2025.04.16 |
|---|---|
| [데이터베이스] 모델링, 관계집합, E-R 다이어그램(ERD), Cardinality (매핑관계) (0) | 2025.04.04 |
| [데이터베이스] 권한과 권한 그룹(역할), 상속, 뷰 권한 (grant, revoke, role) (1) | 2025.04.01 |
| [데이터베이스] 트랜잭션과 무결성 제약 조건, 도메인 (0) | 2025.04.01 |
| [데이터베이스] 뷰(View) 정의와 사용, 삽입 (0) | 2025.03.26 |


댓글