Static Hashing의 기본 개념과 동작 원리
기본 구조
Static hashing은 고정된 수의 bucket을 사용하는 인덱싱 방식이다.
- Bucket은 항목들을 포함하는 저장 공간이다.
- 일반적으로 bucket은 디스크 블록(약 4KB)과 같다.
- Hash function은 bucket의 위치를 찾는 데 사용된다.
- Hash function h는 search-key 집합에서 bucket 주소 집합으로의 함수이다.
- 서로 다른 search-key가 같은 bucket에 매핑될 수 있다.
- Bucket 전체를 순차적으로 검색해야 한다.
인덱스와 파일 구성에서의 사용:
- Hash index에서 bucket은 record 포인터가 있는 항목을 저장한다.
- Hash file-organization에서 bucket은 record 자체를 저장한다.
Static Hashing의 특성
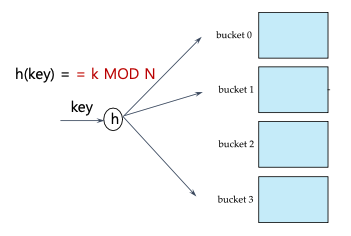
- Bucket(페이지)의 수가 고정되어 있다.
- Bucket은 순차적으로 할당되며, 해제되지 않는다.
- 기본 해시 함수: h(key) = k MOD N (key 값을 N으로 나눈 나머지를 bucket 주소로 사용)
Bucket Overflow 처리
Bucket overflow는 다음과 같은 이유로 발생할 수 있다:
- Bucket의 수가 불충분한 경우
- Record 분포의 편향(skew)
편향이 발생하는 두 가지 이유:
- 여러 record가 동일한 search-key를 가지는 경우
- 선택된 hash function이 key 값의 불균일한 분포를 생성하는 경우
Bucket overflow 확률은 줄일 수 있지만, 완전히 제거할 수는 없다.
Overflow는 일반적으로 overflow bucket을 사용하여 처리한다.
Overflow 처리 방법
1. Overflow chaining:
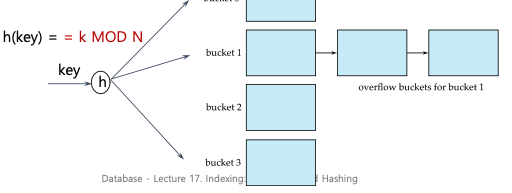
- Overflow bucket들이 연결 리스트로 연결된다.
- 이것은 Closed addressing(Closed hashing)이라고도 불린다.
- 대안으로 open hashing이 있지만, 이는 overflow bucket을 사용하지 않아 데이터베이스 응용에는 적합하지 않다.
2. Linear probing (open hashing)

- 공간이 있는 다음 bucket(순환 순서로)을 사용한다.
- 원래 bucket이 가득 찬 경우, 순환적으로 다음 가용 bucket을 찾는다.
Example of Hash File Organization
Hash File Organization의 예시

- instructor 파일에 대해 dept_name을 key로 사용하는 hash file organization 예시이다.
- i번째 문자의 이진 표현(binary representation)은 정수 i로 간주한다.
- hash function은 각 문자 이진 표현의 합을 10으로 나눈 나머지(modulo 10)로 계산된다.
- 예시:
- h(Music) = 1
- h(History) = 2
- h(Physics) = 3
- h(Elec. Eng.) = 3
- 예시:
- 이 hash function은 uniform distribution(균등 분포)을 제공하지 못한다는 문제가 있다.
Deficiencies of Static Hashing
Static Hashing의 한계
- static hashing에서 hash function h는 search-key를 고정된 bucket address 집합에 매핑한다.
- 데이터베이스는 시간이 지남에 따라 grow(증가) 또는 shrink(감소)할 수 있다.
- bucket 수가 너무 적으면 overflow가 많아져 성능이 저하된다.
- bucket 수가 너무 많으면 bucket이 비게 되어 디스크 공간이 낭비된다.
해결책
- Rehashing:
- 새로운 hash function을 사용하여 파일을 주기적으로 재구성하는 방법이다.
- 비용이 많이 들고, 정상적인 운영을 방해할 수 있다.
- 더 나은 해결책:
- bucket의 수를 동적으로 조정할 수 있도록 허용하는 것이다.
Dynamic Hashing의 종류
Dynamic hashing은 데이터의 양이 동적으로 변할 때 해시 테이블의 크기를 유연하게 조절하는 기법이다. Static hashing과 달리 초기 버킷 수가 고정되지 않으며 데이터 증가에 따라 버킷을 분할하거나 병합하는 방식으로 동작한다. 이 기법은 데이터베이스 시스템에서 디스크 기반 저장소를 효율적으로 관리하기 위해 고안되었다.
대표적으로 Linear Hashing과 Extendible Hashing이 있다.
Linear Hashing은 rehashing(재해싱)을 incremental manner(점진적 방식)로 수행한다. 즉, 한 번에 전체를 재해싱하지 않고, 데이터가 추가될 때마다 필요한 부분만 점진적으로 재해싱한다.
Extendible Hashing은 disk based hashing(디스크 기반 해싱)에 적합하도록 설계된 방식이다. 이 방식에서는 여러 hash value(해시 값)가 하나의 bucket을 공유할 수 있다.
Dynamic Hashing의 핵심 아이디어는 다음과 같다.
- bucket(버킷)의 개수를 2배로 늘릴 수 있다.
- Indirection(간접 참조)의 레벨을 추가한다. 즉, directory of pointers to buckets(버킷을 가리키는 포인터들의 디렉터리)를 사용한다.
- bucket의 개수를 늘릴 때는 directory의 크기를 2배로 만든다.
- overflow(오버플로우)가 발생한 bucket만 분할(split)한다.
- hash function(해시 함수)을 상황에 맞게 조정(adjust)하는 것이 핵심이다.
1. Linear Hashing
Linear hashing은 버킷 오버플로우 발생 시 점진적으로 버킷을 확장하는 방식이다.
전체 해시 테이블을 재구성하지 않고 한 번에 하나의 버킷씩 분할하여 성능 저하를 최소화한다.
분할 메커니즘
next 포인터가 현재 분할할 버킷을 가리키며 오버플로우 발생 시 해당 버킷을 두 개로 나눈다.
분할 후 next 포인터는 다음 버킷으로 이동하며 모든 버킷이 순차적으로 처리되면 라운드가 종료된다. 이 과정에서 해시 함수는 레벨 값에 따라 동적으로 조정되어 새로운 버킷 주소를 계산한다.
2. Extendible Hashing
Extendible Hashing에서는 hash key(해시 키)의 postfix(접미사) 또는 prefix(접두사)만을 사용한다.
- postfix의 길이(즉, 가장 덜 중요한 비트의 개수)를 i bits라고 할 때, 0 ≤ i ≤ 32이다.
- Directory(버킷 주소 테이블)의 크기는 2^i이다.
- 초기에는 i = 0에서 시작한다.
- i의 값은 database(데이터베이스)의 크기가 커지거나 작아짐에 따라 유동적으로 변한다.
- 여러 directory entry(디렉터리 엔트리)가 하나의 bucket을 가리킬 수 있다.
- 실제 bucket의 개수는 2^i보다 작을 수 있다. 이는 bucket의 병합(coalescing)이나 분할(splitting)로 인해 동적으로 변하기 때문이다.
Extendible hashing은 디렉토리 구조를 활용하여 버킷 관리를 최적화하는 방법이다. 해시 키의 비트 패턴을 활용하여 디렉토리 인덱스를 생성하며 버킷 오버플로우 시 디렉토리 크기를 두 배로 확장한다.
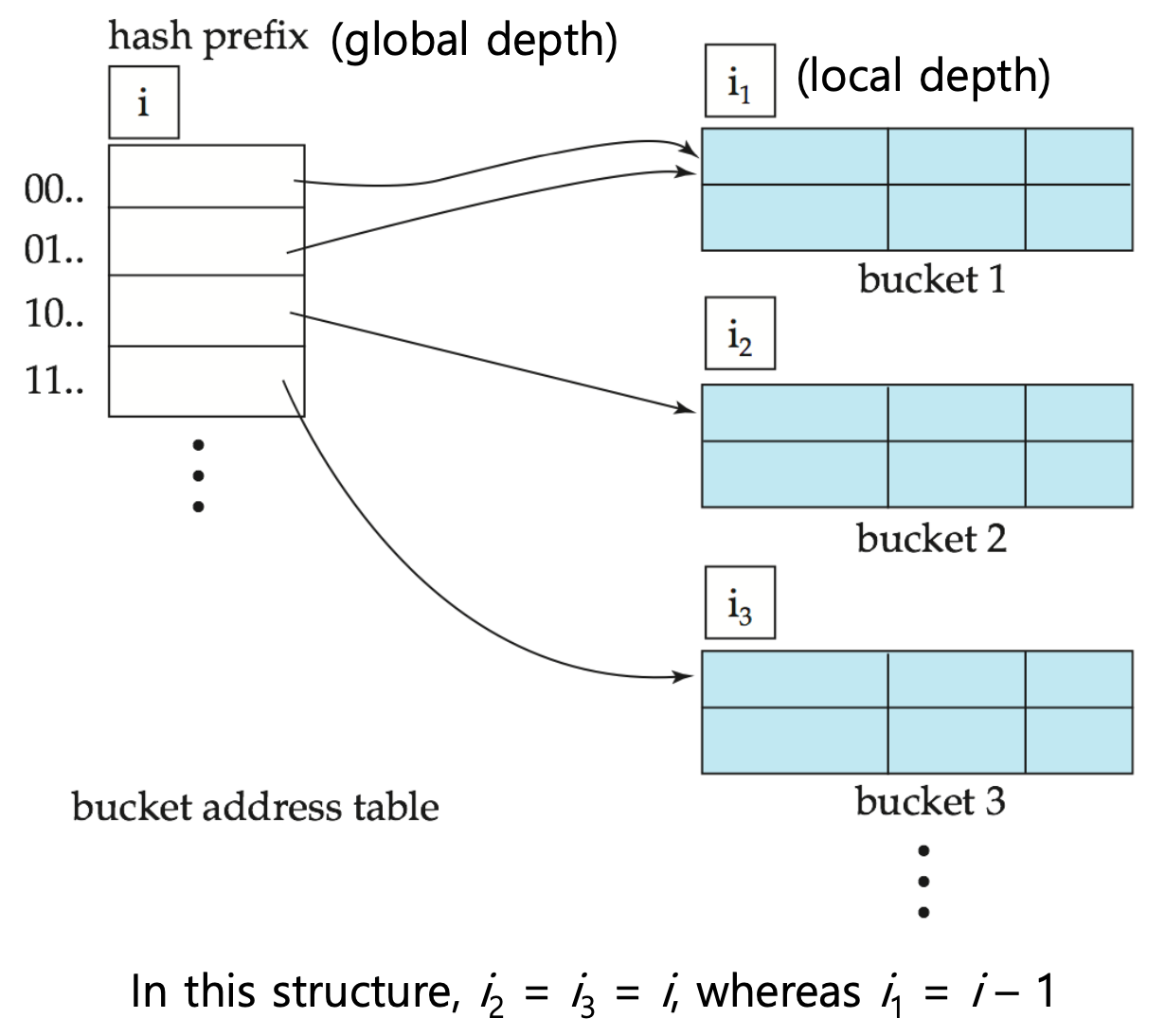
디렉토리 구조
global depth(d)는 해시 값에서 사용할 비트 수를 결정한다. 예를 들어 d=2일 경우 00, 01, 10, 11의 네 개 인덱스로 구성된다.
각 디렉토리 항목은 버킷을 가리키며 여러 항목이 동일한 버킷을 참조할 수 있다.
버킷 분할 과정
버킷이 가득 차면 local depth를 증가시키고 해당 버킷의 레코드를 재분배한다. global depth가 local depth와 동일할 경우 디렉토리 크기를 두 배로 늘린 후 분할을 수행한다. 이때 새로운 디렉토리 항목들은 기존 버킷과 새로 생성된 버킷을 번갈아 가리키도록 업데이트된다.
Extendible Hashing의 작동 원리

키 검색 과정
- 디렉토리는 크기가 4인 배열이므로, 2비트가 필요하다. (2^2 = 4) i=2
- 키 K에 대한 버킷을 찾기 위해 global depth를 사용한다.
- Global depth는 h(K)의 최하위 비트들을 의미한다.
- 예를 들어 h(r) = 5 = 이진수 0101인 경우, 이 키는 01이 가리키는 버킷에 위치한다.
- 또 다른 예로 h(r) = 7 = 이진수 0111인 경우, 이 키는 11이 가리키는 버킷에 위치한다.
예시를 보면, global depth(G)가 2이고 세 개의 버킷이 있다. 첫 번째와 세 번째 버킷은 local depth(L)가 2이며, 두 번째 버킷은 local depth가 1이다. 이는 두 번째 버킷이 01과 11이라는 두 개의 디렉토리 엔트리에서 참조됨을 의미한다.
Bucket Split 과정
버킷 분할은 다음과 같이 진행된다:
G > L인 경우(버킷에 대한 포인터가 여러 개인 경우):
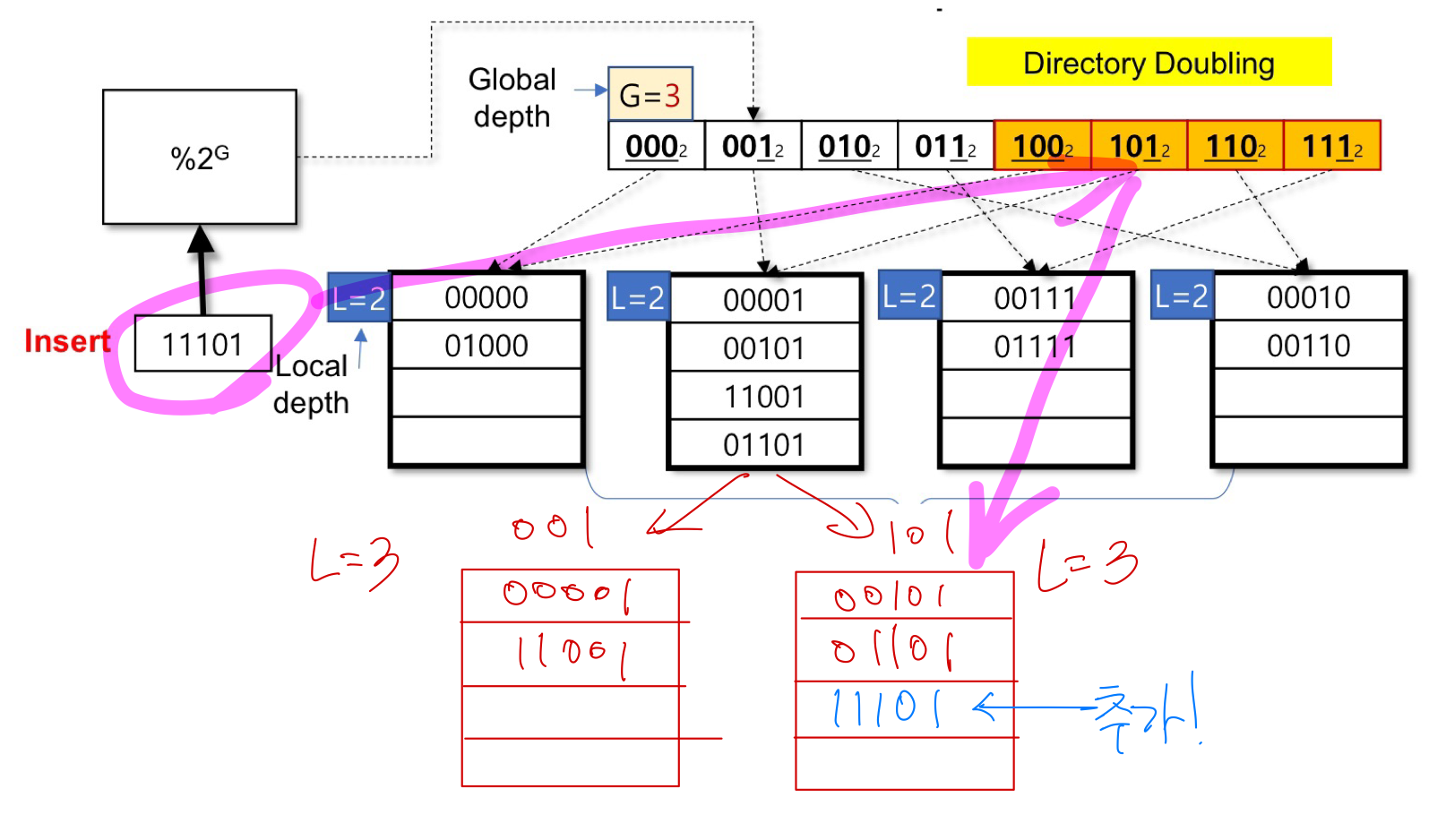
예시에서는 1101 값을 삽입할 때 충돌(collision)이 발생하는 것을 볼 수 있다.
이 예시에서 global depth는 2이고, 해당 키는 01 버킷에 매핑되어야 하지만 이미 가득 찬 상태이다.
이 경우 버킷을 분할하고 디렉토리를 재구성하는 과정이 필요하다.
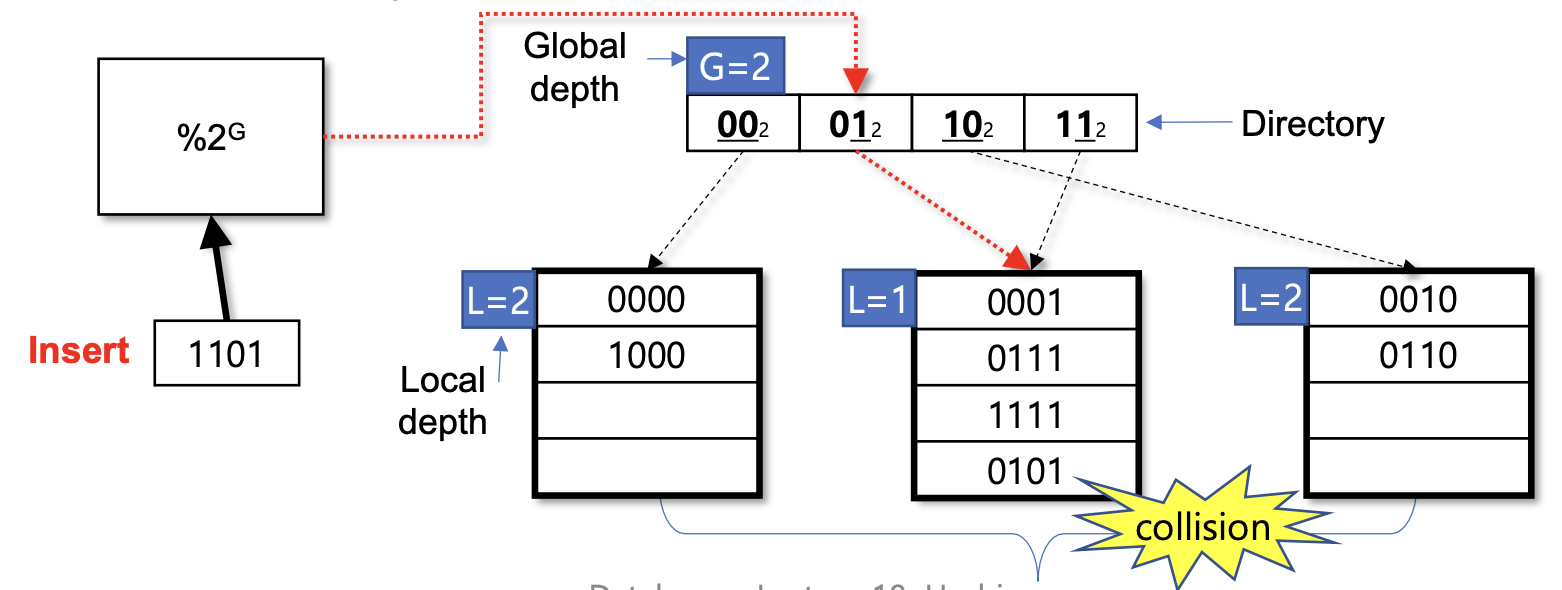

- 새로운 버킷을 할당하고, L = L+1로 설정한다.
- 디렉토리를 업데이트하여 새 버킷을 가리키도록 한다.
- 오버플로우된 버킷의 레코드들을 새 버킷으로 이동한다.
- 버킷이 여전히 가득 차 있으면 추가 분할이 필요하다.
G = L인 경우 (버킷에 대한 포인터가 하나만 존재하는 경우) -> Directory Doubling
예시를 보면, 초기에 G=2인 상태에서 디렉토리는 00, 01, 10, 11의 네 개 엔트리로 구성되어 있다.
11101 값을 삽입하려고 할 때 해당 버킷은 이미 가득 차 있어 split이 필요하다.
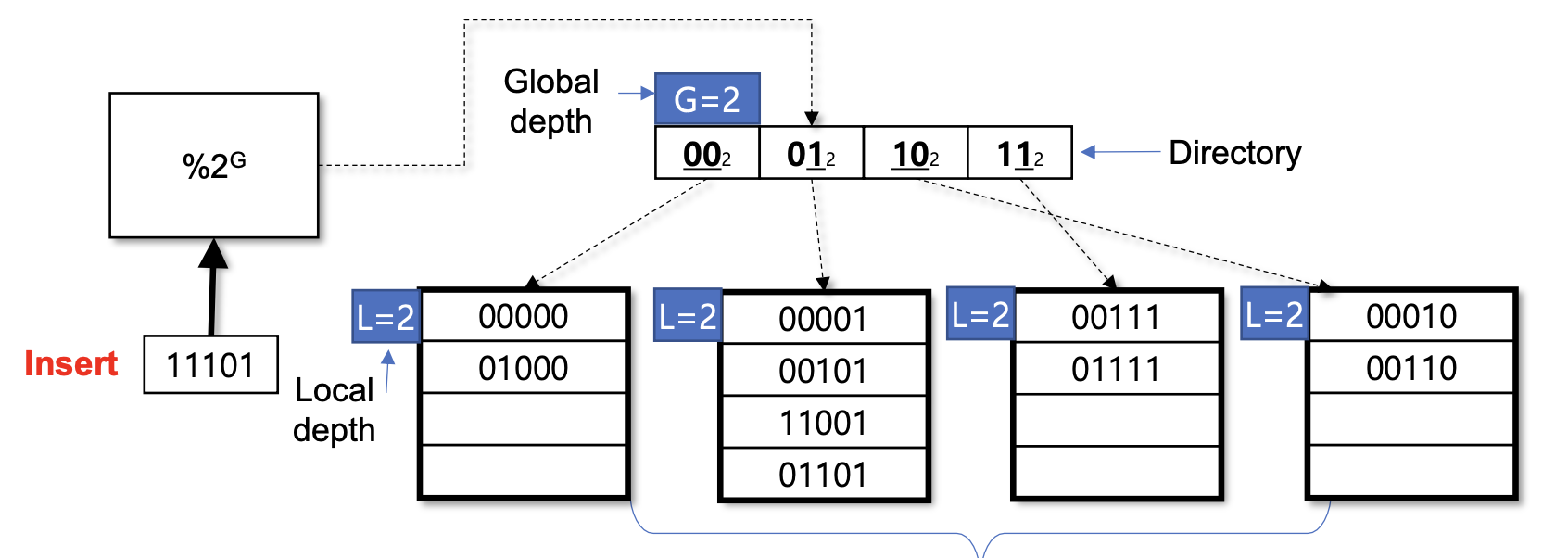
G = L인 상황에서 버킷 오버플로우가 발생하면 다음과 같은 단계로 처리한다:
- Global depth(G)를 1 증가시키고 디렉토리 크기를 두 배로 확장한다.
- 기존 각 엔트리를 동일한 버킷을 가리키는 두 개의 엔트리로 대체한다.
- 이 과정 이후 G > L 상태가 되어 이전 슬라이드에서 설명한 첫 번째 경우를 적용할 수 있다.
Directory Doubling 과정
디렉토리 크기가 두 배로 확장된 후 새로운 엔트리들(100, 101, 110, 111)이 추가되었다. 이렇게 확장된 디렉토리를 통해 더 많은 버킷 포인터를 관리할 수 있게 된다.
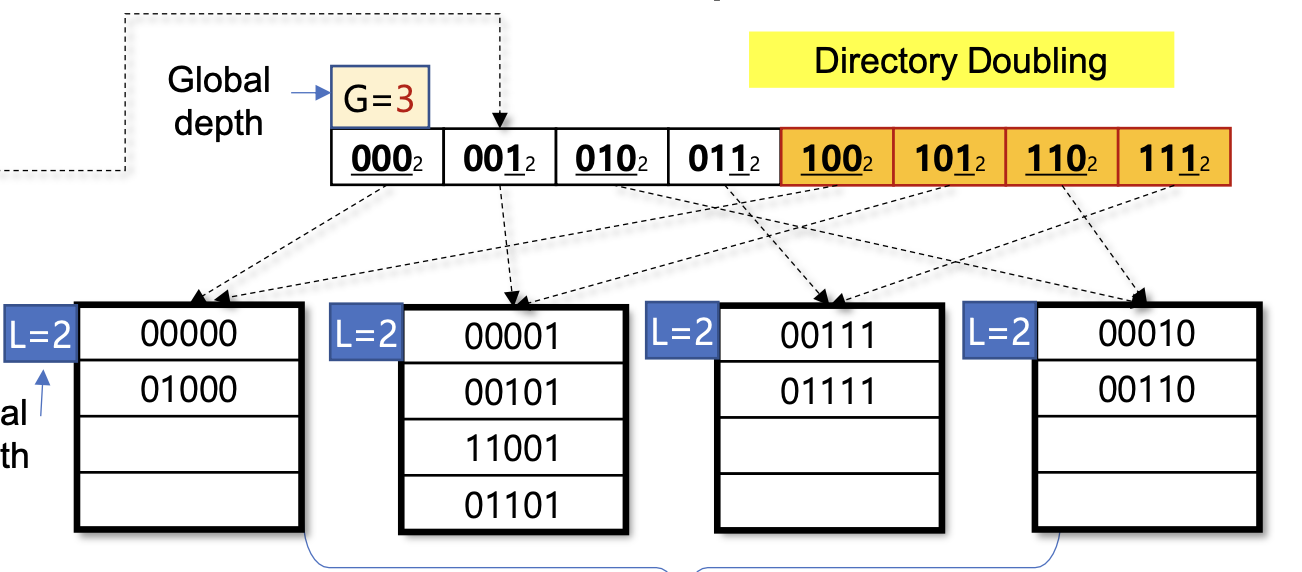
Directory doubling은 다음과 같이 진행된다:
- Global depth가 2에서 3으로 증가하면서 디렉토리 크기는 4에서 8로 확장된다.
- 새로운 디렉토리는 000, 001, 010, 011, 100, 101, 110, 111의 8개 엔트리로 구성된다.
- 기존에는 앞에 0으로 추가하고, 이후에는 1씩 앞에 추가해서 뒤에 삽입한다.
- 기존 디렉토리의 각 엔트리는 두 개의 새 엔트리로 확장된다:
- 00 → 000, 100
- 01 → 001, 101
- 10 → 010, 110
- 11 → 011, 111
- 이후 G > L 상태가 되어 버킷 분할이 가능해진다.
Directory Doubling 과정 후, G > L 상태에서 버킷 분활한 모습
Extendible Hashing의 장단점
Extendible Hashing 장점
- 파일 크기가 증가해도 해시 성능이 저하되지 않는다. (접근 한번으로 가능하다)
- 공간 오버헤드가 최소화된다.
Extendible Hashing 단점
- 원하는 레코드를 찾기 위해 간접 참조 레벨이 추가된다. -> 디렉토리 배열을 말한다.
- Bucket address table(디렉토리)이 매우 커질 수 있으며, 때로는 메모리 크기보다 더 커질 수도 있다.
- 디스크에 큰 연속 영역을 할당할 수 없는 문제가 발생할 수 있다.
- 이 문제의 해결책으로 B+-tree 구조를 bucket address table에 적용할 수 있다.
- Bucket address table의 크기 변경은 비용이 많이 드는 작업이다.
Linear Hashing과의 비교
Linear hashing은 Extendible hashing의 대안으로 사용될 수 있는 메커니즘이다:
- 점진적인 성장을 허용한다.
- 하지만 더 많은 버킷 오버플로우가 발생할 수 있다는 단점이 있다.
Extendible hashing은 데이터베이스 시스템에서 디스크 기반 인덱싱을 위한 효과적인 방법이지만, 특정 상황에서는 Linear hashing과 같은 대안을 고려할 필요가 있다. 시스템의 요구사항과 데이터 특성에 따라 적절한 해싱 기법을 선택하는 것이 중요하다.
Linear Hashing
Linear Hashing은 디렉토리를 사용하지 않고도 긴 overflow chain 문제를 해결하는 lazy approach 방식의 동적 해싱 기법입니다.
이 방식은 임시 overflow 페이지를 활용하며, 분할할 버킷을 round-robin 방식으로 선택하는 특징이 있습니다.
Linear Hashing의 기본 개념
Linear Hashing에서는 어떤 버킷이 overflow될 때, 실제로 분할되는 버킷은 "Next" 포인터가 현재 가리키고 있는 버킷입니다.(직전에 오버플로우한 버킷은 절대 아니다.)
분할 후에는 이 포인터를 다음 버킷으로 이동시킵니다. 이 방식은 다음과 같은 해시 함수 계열을 사용합니다:
- hi(key) = h(key) mod(2^i*N)
- N은 초기 버킷 수로, 반드시 2의 제곱수여야 합니다
- hi+1은 hi의 범위를 두 배로 늘리는데, 이는 디렉토리 더블링과 유사한 방식입니다
Linear Hashing 알고리즘
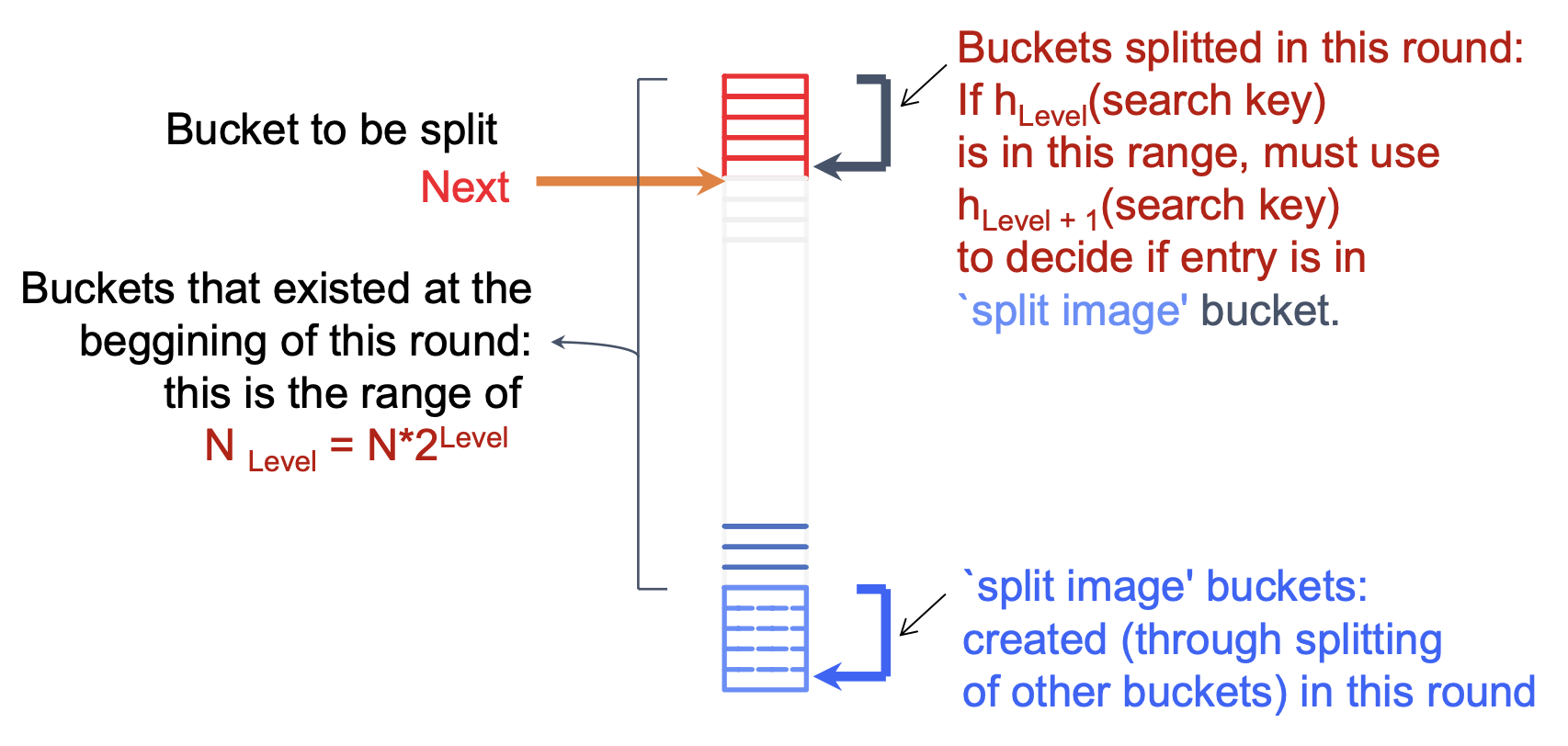
Linear Hashing 알고리즘은 'round'라고 부르는 단계별로 진행됩니다. 현재 round 번호는 "Level"이라고 합니다. 한 round의 시작 시점에서는 NLevel = N * 2^Level 개의 버킷이 존재합니다. 여기서 N은 초기 버킷 수(N0)를 의미합니다.
알고리즘이 진행되는 동안:
- 0부터 Next-1까지의 버킷들은 이미 분할된 상태입니다
- Next부터 NLevel까지의 버킷들은 현재 round에서 아직 분할되지 않았습니다
모든 초기 버킷이 분할되면 해당 round가 종료됩니다. 즉, Next = NLevel 조건이 만족되면 round가 끝납니다.
다음 round를 시작하기 위해서는:
Level++;
Next = 0;
위 과정을 수행합니다.
Linear Hashing - 삽입 연산
Linear Hashing에서 데이터 삽입 과정은 다음과 같습니다:
- 적절한 버킷을 찾고, 공간이 있으면 데이터를 삽입하고 종료합니다.
- 공간이 없는 경우:
- 임시 overflow 페이지를 추가하고 해당 페이지에 데이터 항목을 삽입합니다.
- Next 버킷을 분할하고 Next 값을 증가시킵니다.
- 이때 분할되는 버킷은 방금 overflow가 발생한 버킷이 아닐 가능성이 높습니다.
- 분할 후에는 hLevel+1 해시 함수를 사용하여 항목들을 재분배합니다.
버킷들이 round-robin 방식으로 분할되기 때문에, 긴 overflow chain이 생길 가능성이 있습니다.
43(101011₂) 삽입 과정 (Level 0, N=4)

초기 상태에서는 4개의 버킷이 있고, 각 버킷은 h₀ 함수를 사용하여 접근합니다.
h₀ 함수는 key를 4로 나눈 나머지(mod 4)를 계산합니다. 즉, 2비트 값(00, 01, 10, 11)이 버킷 인덱스가 됩니다.
43을 삽입할 때:
- 43 mod 4 = 3 이므로 버킷 3(11₂)에 배정됩니다.
- 버킷 3에는 이미 31, 35, 7, 11이 있어 공간이 부족합니다.
- 그 결과 overflow page가 생성되어 43이 저장됩니다.
- Next 포인터는 버킷 0을 가리키고 있었으므로, 버킷 0을 split하고 Next는 1로 이동합니다.
- 분할로 인해 버킷 0에 있던 32, 44, 36 중 44와 36이 새로운 버킷 4(100₂)로 재배치됩니다.
6(110₂) 삽입 과정 (Level 0, N=4)
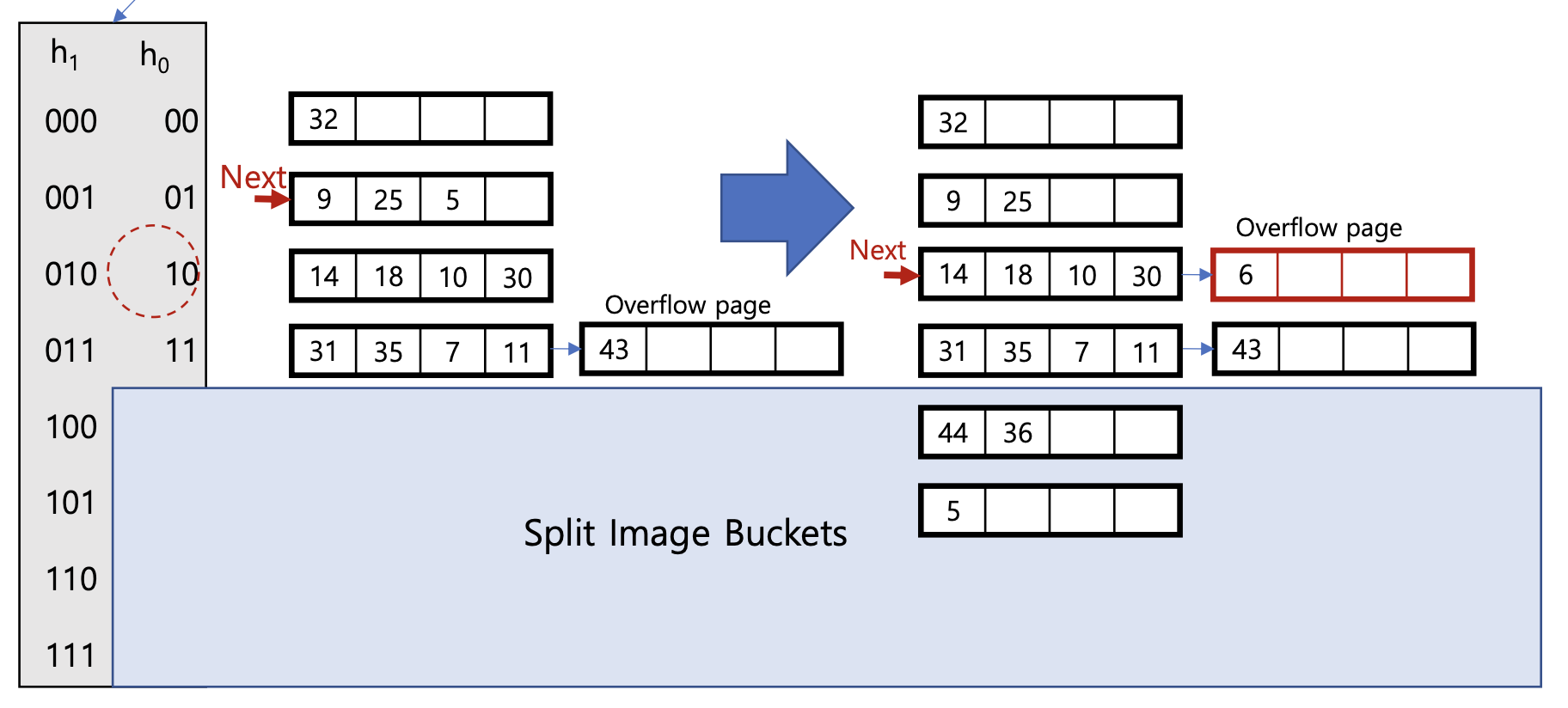
이전 상태에서 6을 삽입합니다:
- 6 mod 4 = 2 이므로 버킷 2(10₂)에 배정됩니다.
- 버킷 2에는 이미 14, 18, 10, 30이 있어 공간이 부족합니다.
- overflow page가 생성되어 6이 저장됩니다.
- Next 포인터는 현재 버킷 1을 가리키고 있으므로, 버킷 1을 split하고 Next는 2로 이동합니다.
- 분할로 인해 버킷 1에 있던 9, 25, 5 중 5가 새로운 버킷 5(101₂)로 재배치됩니다.
Linear Hashing의 특징
Linear Hashing에서는 overflow가 발생하더라도 반드시 overflow가 발생한 버킷을 바로 split하지는 않습니다.
대신 Next 포인터가 가리키는 버킷을 순차적으로 split하여 점진적으로 hash table의 크기를 확장합니다. 이러한 방식은 다음과 같은 특징이 있습니다:
- 해시 함수가 Level에 따라 달라집니다: h₀, h₁, h₂ 등
- Split되는 버킷은 round-robin 방식으로 결정됩니다
- Overflow가 발생한 버킷과 실제로 split되는 버킷이 다를 수 있습니다
- 점진적인 확장을 통해 한 번에 전체 테이블을 재구성하는 부담을 줄일 수 있습니다
이와 같이 Linear Hashing은 데이터 증가에 따라 효율적으로 hash table의 크기를 조절할 수 있는 dynamic hashing 기법입니다.
Linear Hashing의 Search 예시
Linear Hashing에서 데이터를 검색하는 방법은 해당 데이터 항목이 어느 버킷에 속하는지 결정하는 것부터 시작합니다.
데이터 항목 r에 대해 적절한 버킷을 찾기 위해서는 hLevel(r) 함수를 사용합니다.
검색 과정은 버킷의 분할 상태에 따라 달라집니다:
- 아직 분할되지 않은 버킷의 경우:
- hLevel(r) >= Next 조건이 성립하면(즉, hLevel(r)이 현재 round에서 아직 분할에 관여하지 않은 버킷인 경우), r은 확실히 그 버킷에 속합니다.
- 이미 분할된 버킷의 경우:
- r은 두 가지 버킷 중 하나에 속할 수 있습니다: hLevel(r) 또는 hLevel(r) + NLevel
- 실제로 어느 버킷에 속하는지 확인하기 위해서는 hLevel+1(r) 함수를 적용해야 합니다.
Linear Hashing Search동작 예시

예를 들어, Level 0, N=4인 상태에서 5(00101₂)를 검색하는 과정을 살펴보겠습니다:
해당 해시 함수는 다음과 같습니다: hLevel(key) = h(key) mod(2^Level*N)
이 상태에서:
- 버킷 00과 01은 이미 분할되어 버킷 100와 101가 생성되었습니다.
- Next 포인터는 버킷 2를 가리키고 있습니다.
- 5에 대해 h0(5) = 5 mod 4 = 01입니다.
- 그러나 버킷 1은 이미 분할되었으므로, h1(5) = 5 mod 8 = 101를 사용하여 버킷 5에 속한다는 것을 확인할 수 있습니다.
이처럼 Linear Hashing 검색 알고리즘은 버킷의 분할 상태를 고려해 데이터가 어느 버킷에 위치하는지 정확히 찾을 수 있습니다.
Ordered Indexing과 Hashing의 비교
데이터베이스 인덱싱 방법을 선택할 때는 다음과 같은 요소들을 고려해야 합니다:
- 주기적 re-organization 비용
- Hashing은 버킷 분할이 발생할 때 일부 데이터만 재배치하므로 전체 재구성 비용이 분산됩니다.
- 삽입과 삭제의 상대적 빈도
- 빈번한 삽입/삭제 환경에서는 동적으로 대응할 수 있는 Linear Hashing이 효율적일 수 있습니다.
- 평균 access time과 worst-case access time 간의 최적화 선택
- Hashing은 평균적으로 O(1) 접근 시간을 제공하지만, collision이나 overflow로 인한 worst-case 성능은 좋지 않을 수 있습니다.
- 쿼리 유형:
- Hashing은 point query에 일반적으로 더 효율적입니다
- Range query가 빈번하다면 ordered indices가 더 적합합니다
- 실제 데이터베이스 시스템에서의 구현:
- PostgreSQL은 hash indices를 지원하지만 성능 문제로 사용을 권장하지 않습니다
- Oracle은 static hash organization을 지원하나 hash indices는 지원하지 않습니다
- SQL Server는 B+-trees만을 지원합니다
Linear Hashing은 동적으로 해시 테이블 크기를 조절할 수 있어 효율적인 점이 장점이지만, range query가 필요한 경우나 최악의 경우 성능이 중요한 경우에는 ordered indexing 방법이 더 적합할 수 있습니다.
Multiple-Key Access와 Bitmap Index 구조
Multiple-Key Access는 특정 유형의 쿼리에서 여러 인덱스를 활용하는 방법입니다. 이를 통해 복합 조건을 가진 쿼리 처리 성능을 향상시킬 수 있습니다.
다중 인덱스 접근 전략
특정 쿼리를 처리할 때 여러 인덱스를 활용하는 전략을 살펴보겠습니다. 예를 들어, 다음과 같은 쿼리가 있다고 가정해봅시다:
select ID
from instructor
where dept_name = "Finance" and salary = 80000
이 쿼리를 처리하기 위한 가능한 전략은 다음과 같습니다:
- dept_name 인덱스를 사용하여 Finance 학과 소속 강사들을 찾은 다음, salary = 80000 조건을 테스트합니다.
- salary 인덱스를 사용하여 급여가 $80000인 강사들을 찾은 다음, dept_name = "Finance" 조건을 테스트합니다.
Bitmap Index의 개념과 특징
Bitmap index는 여러 key에 대한 쿼리를 효율적으로 처리하기 위해 설계된 인덱스 구조입니다. 이 구조는 다음과 같은 특징을 가집니다:
- 레코드는 0부터 시작하는 순차적 번호가 부여된다고 가정합니다.
- 고정 크기 레코드일 때 특히 레코드 검색이 용이합니다.
- 주로 적은 수의 distinct value를 가지는 속성에 적용됩니다.
- 예: gender, country, state 등
- income-level처럼 소수의 범주로 나눌 수 있는 값(0-9999, 10000-19999 등)에도 적용 가능합니다.
가장 기본적으로, bitmap은 단순한 비트 배열입니다.
Bitmap Index의 구조
Bitmap index는 속성의 각 값마다 하나의 bitmap을 가지고 있습니다. 각 bitmap은 레코드 수만큼의 비트를 포함합니다.
- 특정 값 v에 대한 bitmap에서, 레코드 r이 해당 속성에 대해 값 v를 가지면 비트 값은 1이고, 그렇지 않으면 0입니다.
예를 들어, gender와 income_level에 대한 bitmap 구조는 다음과 같습니다:
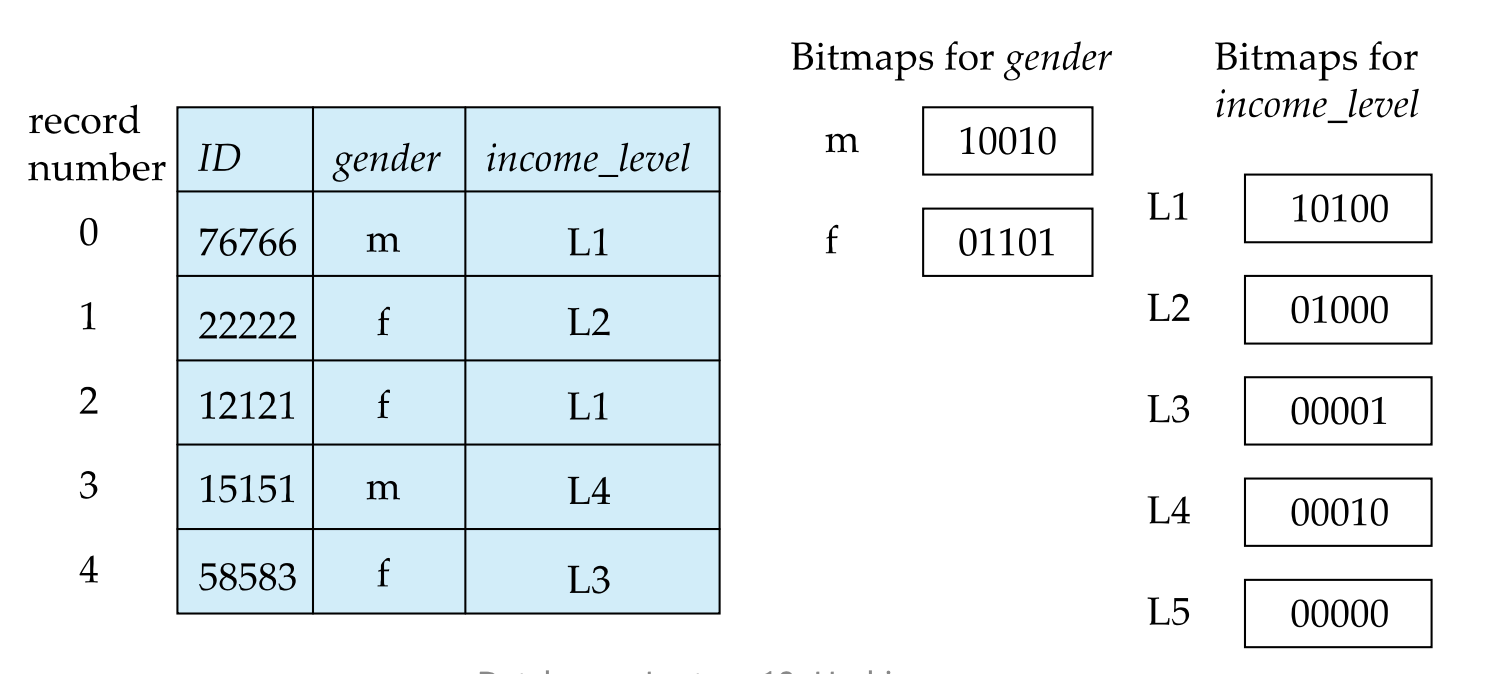
- gender 'f'에 대한 bitmap: 01101 (레코드 1, 2, 4가 여성임을 표시)
- income_level 'L1'에 대한 bitmap: 10100 (레코드 0, 2가 L1 소득 수준임을 표시)
Bitmap 연산을 통한 쿼리 처리
Bitmap index는 특히 여러 속성에 대한 쿼리에 유용하지만, 단일 속성 쿼리에는 특별히 효율적이지 않습니다. 쿼리는 다음과 같은 bitmap 연산을 통해 처리됩니다:
- Intersection (and)
- Union (or)
각 연산은 같은 크기의 두 bitmap을 입력받아 해당 비트별 연산을 수행하여 결과 bitmap을 생성합니다.
예시:
- 100110 AND 110011 = 100010
- 100110 OR 110011 = 110111
- NOT 100110 = 011001
실제 활용 예시로, 남성이면서 소득 수준 L1인 레코드를 찾는 쿼리:
- Males: 10010 (레코드 0, 3이 남성)
- Income level L1: 10100 (레코드 0, 2가 L1)
- 결과: 10010 AND 10100 = 10000 (레코드 0만 조건 충족)
이렇게 얻어진 bitmap을 통해 필요한 튜플을 검색할 수 있으며, 일치하는 튜플 수를 계산하는 것도 매우 빠르게 수행할 수 있습니다.
Bitmap Index의 효율성
Bitmap index는 일반적으로 관계형 테이블 크기에 비해 매우 작습니다:
- 예를 들어, 레코드 크기가 100바이트라면, 하나의 bitmap은 관계형 테이블 공간의 약 1/800만 사용합니다.
- 만약 distinct 속성 값이 8개라면, 전체 bitmap index는 관계형 테이블 크기의 약 1%에 불과합니다.
이러한 공간 효율성과 빠른 비트 연산 처리 능력은 특정 유형의 쿼리에서 Bitmap index가 매우 효율적인 선택이 될 수 있게 합니다.




댓글