나무 자르기
문제
상근이는 나무 M미터가 필요하다. 근처에 나무를 구입할 곳이 모두 망해버렸기 때문에, 정부에 벌목 허가를 요청했다. 정부는 상근이네 집 근처의 나무 한 줄에 대한 벌목 허가를 내주었고, 상근이는 새로 구입한 목재절단기를 이용해서 나무를 구할것이다.
목재절단기는 다음과 같이 동작한다. 먼저, 상근이는 절단기에 높이 H를 지정해야 한다. 높이를 지정하면 톱날이 땅으로부터 H미터 위로 올라간다. 그 다음, 한 줄에 연속해있는 나무를 모두 절단해버린다. 따라서, 높이가 H보다 큰 나무는 H 위의 부분이 잘릴 것이고, 낮은 나무는 잘리지 않을 것이다. 예를 들어, 한 줄에 연속해있는 나무의 높이가 20, 15, 10, 17이라고 하자. 상근이가 높이를 15로 지정했다면, 나무를 자른 뒤의 높이는 15, 15, 10, 15가 될 것이고, 상근이는 길이가 5인 나무와 2인 나무를 들고 집에 갈 것이다. (총 7미터를 집에 들고 간다) 절단기에 설정할 수 있는 높이는 양의 정수 또는 0이다.
상근이는 환경에 매우 관심이 많기 때문에, 나무를 필요한 만큼만 집으로 가져가려고 한다. 이때, 적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 나무의 수 N과 상근이가 집으로 가져가려고 하는 나무의 길이 M이 주어진다. (1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000)
둘째 줄에는 나무의 높이가 주어진다. 나무의 높이의 합은 항상 M보다 크거나 같기 때문에, 상근이는 집에 필요한 나무를 항상 가져갈 수 있다. 높이는 1,000,000,000보다 작거나 같은 양의 정수 또는 0이다.
출력
적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 출력한다.
예제 입력 1
4 7
20 15 10 17
예제 출력 1
15
예제 입력 2
5 20
4 42 40 26 46
예제 출력 2
36java 코드
이 문제는 이분탐색(매개변수탐색)을 이용하는 문제입니다.
mid 값 그대로 비교하는것이 아니라 mid값을 대입해서 나무의 길이를 구해서 mid를 올릴지 내릴지 결정하는 것이므로 엄밀히 말하면 매개변수 탐색이 맞는데, 매개변수 탐색이 어려운 용어이고 이분탐색의 개념만 알아도 응용해서 풀수있기 때문에 이렇게 코드를 짰습니다.
- 나중에 매개변수 탐색으로 푸는 글도 올리겠습니다.
절단기의 높이 H의 최댓값을 구하는것인데, 절단기의 높이를 너무 길게하면 충분한 나무를 못얻고, 너무 낮추면 너무 많은 나무가 잘리게 됩니다.
절단기의 높이 H의 최소값을 1 , 절단기의 높이 H의 최댓값을 가장 큰 나무의 길이로 지정해서 M미터 이상의 나무를 자를수 있도록 이분 탐색을 해서 구할것입니다.
이분탐색에 대한 설명은 아래에 있습니다.
<알고리즘>
- 처음 low값을 1로, high값을 나무 중 가장 큰 나무의 길이로 지정해줍니다.
- mid값을 구하고 이분 탐색을 통해 얻을수 있는 나무의 길이를 구합니다.
- 얻을수 있는 나무의 길이가 요구되는 나무의 길이보다 많거나 같다면 절단기 높이 H를 높힙니다. (low = mid + 1)
- 이 과정에서는 나무 길이의 최댓값을 계속 업데이트해줍니다.
- 얻을수 있는 나무의 길이가 요구되는 나무보다 작다면 절단기의 높이 H를 낮춥니다. (high = mid - 1)
- 얻을수 있는 나무의 길이가 요구되는 나무의 길이보다 많거나 같다면 절단기 높이 H를 높힙니다. (low = mid + 1)
- while문이 종료되고 절단기의 최대 높이 H를 출력합니다.
import java.util.Scanner;
//Silver_2805.java
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt(); // numbers of trees
int m = scan.nextInt(); // need m meters
int[] trees = new int[n]; //height of trees
int MAX = 0;
for (int i = 0; i < n; i++) {
trees[i] = scan.nextInt();
if (trees[i]>MAX) {
MAX = trees[i];
}
}
scan.close();
int low = 0;
int high = MAX;
int H = 0; //answer
while (low<=high) {
int mid = (low+high)/2;
long count = 0; //gained trees
for (int tree : trees) {
if(tree>mid)
count+= (tree - mid);
}
if (m <= count) {
low = mid + 1;
if(mid >= H) //higher the better
H = mid;
}
else{// m > count
high = mid - 1;
}
}
System.out.println(H);
}
}이분 탐색 (이진탐색)
이분탐색은 검색 범위를 줄여 나가면서 원하는 데이터를 검색하는 알고리즘입니다.
오름차순으로 정렬된 정수의 리스트를 같은 크기의 두 부분 리스트로 나누고 필요한 부분에서만 탐색하도록 제한하여 원하는 원소를 찾는 알고리즘입니다.
리스트의 중간 부분에 찾는 원소가 있는지 확인하고, 없으면 위쪽에 있는지 아래쪽에 있는지 판단하여 맨 앞부터 검색하거나 중간부터 검색합니다.
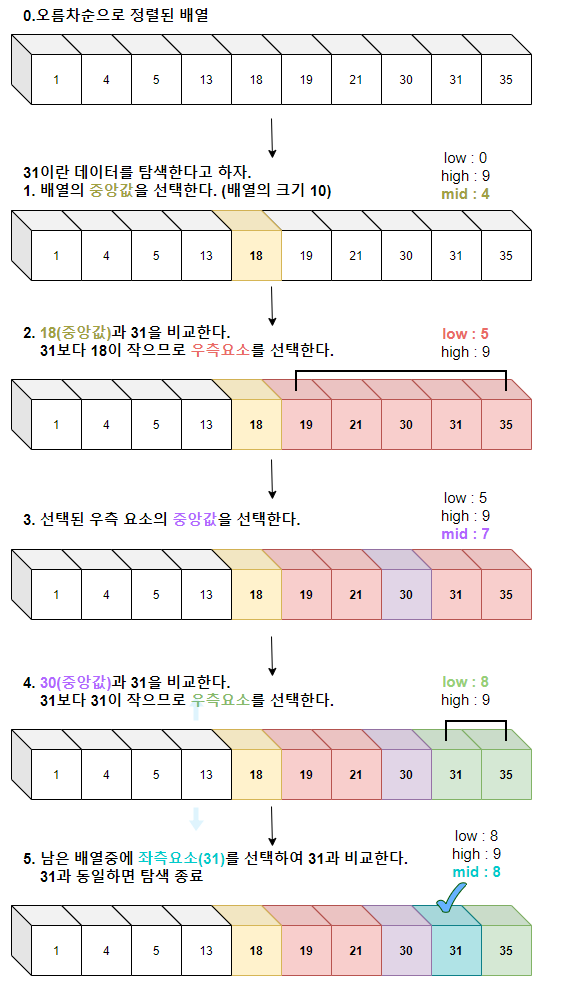
아래는 이분 탐색을 구현한 자바코드입니다.
정렬된 배열을 받으면 mid으로 탐색하면서 범위를 좁혀가면서 알맞는 인덱스를 반환합니다.
public static int binarySearch_loop(int[] arr, int target) {
int low = 0;
int high = arr.length-1;
int mid = 0;
// 제일 작은수가 큰수보다 커지면 탐색 종료
while(low <= high) {
mid = (low + high) /2; // 1번 과정 : 중앙값 찾기
if(arr[mid] == target) {
return mid;
}else if(arr[mid] > target) { // 현재의 중앙값보다 작으면,
high = mid-1; // 왼쪽요소를 선택하기 위해 high = mid -1로 설정
}else {
low = mid+1; // 현재의 중앙값보다 크면, 오른쪽 요소를 선택하기 위해 low = mid+1로 설정
}
}
// 탐색해도 결과가 없는 경우
return -1;
}'알고리즘 PS (백준) > ☕️ Java (자바)' 카테고리의 다른 글
| [백준 11279] 우선순위 큐 + Comparator - java(자바) 최대 힙 (0) | 2022.08.16 |
|---|---|
| [백준 1927] 우선순위 큐 java(자바) - 최소 힙 (0) | 2022.08.11 |
| [백준 1654] 이분탐색 java(자바) - 랜선 자르기 (0) | 2022.08.04 |
| [백준 7568] 덩치 - java(자바) 브루트포스 알고리즘 (0) | 2022.08.02 |
| [백준 2839] 설탕 배달 java(자바) - 그리디 알고리즘 (0) | 2022.07.28 |



댓글